[next] [prev] [prev-tail] [tail] [up]

1.16 The areal velocity.

The rate at which the radius vector from a fixed point to the moving particle describes a surface is called the areal velocity with respect to the point. Suppose the particle moves in the xy plane.

PIC

Let ΔA represent the area of the triangle OPQ swept over by the radius vector in the interval of time Δt. Then

r′ ⋅r ΔA = 2 sin(Δθ )

whence

′ ΔA--= r-⋅r-⋅ sin(Δ-θ) ⋅ Δ-θ Δt 2 Δθ Δt
(1.26)

As the angle ΔA diminishes the ratio of the area of the triangle to that of the sector approaches unity as a limit. The limit of r′ is r, and the limit of sin(Δθ) Δθ is unity. Equation (1.26) gives, on passing to the limit Δt = 0 in both members,

dA--= 1-r2dθ- dt 2 dt
(1.27)

as the expression for the areal velocity. On changing to rectangular coordinates by the substitution

∘ -------- r = x2 + y2, tan θ = y- x

equation (1.27) becomes

( ) dA 1 dy dx ----= -- x---- y--- dt 2 dt dt
(1.28)

If the motion is not in the xy plane the projections of the areal velocity upon the three fundamental planes are used. They are respectively

( ( ) ||| dAxy- = 1- xdy-- ydx- ||| dt 2 dt dt |{ dAyz 1 ( dz dy ) ----- = -- y---- z--- ||| dt 2 ( dt dt ) |||| dAzx 1 dx dz ( -dt-- = 2- zdt-- xdt-
(1.29)

In certain mechanical problems the body considered moves so that the areal velocity is constant if the origin is properly chosen. In this case it is said that the body obeys the law of areas with respect to the origin. That is,

2dθ- r dt = constant

It follows from this equation and (1.19) that in this case

αθ = 0

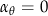
that is, the acceleration perpendicular to the radius vector is zero.

[next] [prev] [prev-tail] [front] [up]